空間分割 - デカルト積を回避しながらポリゴンデータの結合・解析を効率化する方法

このブログでは、オードナンス・サーベイ（Ordnance Survey、英国陸地測量部）、データブリックス、Microsoft が共同で取り組む British National Grid（BNG）を用いた空間分割について解説します。

オードナンス・サーベイは、公共部門地理空間協定（Public Sector Geospatial Agreement）に基づき、グレートブリテン島（GB）を対象とする新たな全国地理データベース（NGD：National Geographic Database）のデータ配信を設計・開発しています。

オードナンス・サーベイでは、コアデータサービスプラットフォームの一環として、データブリックスおよび Microsoft と緊密に連携し、全国地理データベース（NGD）を支えるアーキテクチャ戦略の構築とデータエンジニアリングのケイパビリティの強化に取り組んできました。このプラットフォームにより、オードナンス・サーベイは、従来オンプレミスのマシン上でシングルスレッドのプロセス行われていた地理空間データの処理や FME などのアプリケーションを、クラウドコンピューティングなどのスケーラブルなオンデマンドで利用できるようになり、大規模な地理空間データの処理・分析（解析）が実現します。オードナンス・サーベイでは、Apache Spark™ のケイパビリティをクラウドプラットフォームに追加するために Azure Databricks を利用しています。このことが、データとアプローチの両方の最適化、および並列処理を使用した大規模な地理空間結合の実行について考え直すきっかけとなりました。

空間データの適切なインデックス化は、このような最適化作業の一環であり、インデックスの選択だけで作業が完了するわけではありません。このブログでは、Azure Databricks が提供するオプティマイザーが大規模な地理空間結合時にディスクからのデータ読み込みをチューニングするために、インデックスを最大限に活用する私たちが設計したプロセスについて解説します。

地理空間を識別子の付いたビンに分割するグリッドインデックスには、BNG、Geohash、Uber の H3、Google の S2 など、さまざまなものがあります。これらのうちのいくつかは、最新の地理空間分析（解析）にともなって開発されたため、関連するライブラリや実際の分析での使用例が十分に用意されている傾向にあります。一方、British National Grid （BNG）インデックスシステムは 1936 年に策定され、グレートブリテン島の地理空間データエコシステムに深く組み込まれていますが、大規模な地理空間分析を目的とした利用や公開は行われていません。そこで今回は、グレートブリテン島の地理空間データを他のインデックスシステムに変換することなく、BNG を空間結合の最適化に直接使用できることを示すことも目的にしました。ポリゴンを分割し、該当する BNG インデックスにおける位置情報と結びついたシンプルなジオメトリに変換するモザイク法の実装を行っています。このアプローチにより、インデックス空間の比較と空間述語の評価を効果的に制限できるようになり、クエリのパフォーマンスが大幅に改善されました。

ポイントインポリゴンの難しさ

あるポイントがポリゴン内にあるかどうかの判別、ポイントインポリゴン（PIP: Point in Polygon）の難易度はどのくらいでしょうか？PIP の判別方法は既に確立されており、容易な問題だと捉えられがちです。しかし、テクノロジーが進化して並列システムが導入されるようになると、PIP を別の観点から考える必要性が出てきました。例えば、膨大な地理空間データの結合関係として PIP を使用するケースです。高レベルの並列性を確保することが課題となりますが、従来の手法はこのケースには不向きなのです。

結合関係はペアリングの問題と捉えることができます。すなわち、2 つのデータセットがある場合に、結合条件を満たしつつ、他方のデータセットの行セットと一致する行が含まれる関係と解釈できます。結合関係の複雑さは O(n*m) です。これは一般にデカルト積（複雑性）として知られるものです。最も複雑な結合関係であり、簡単に言えば、全ての一致を解決するために、一方のデータセットの各レコードと他方のデータセットの各レコードを比較する必要があることを意味します。多くのシステムで、この複雑さを低く抑えるための技術や経験則による対応が実装されていますが、これが基本になります。今回はこの基本から考察を始めます。

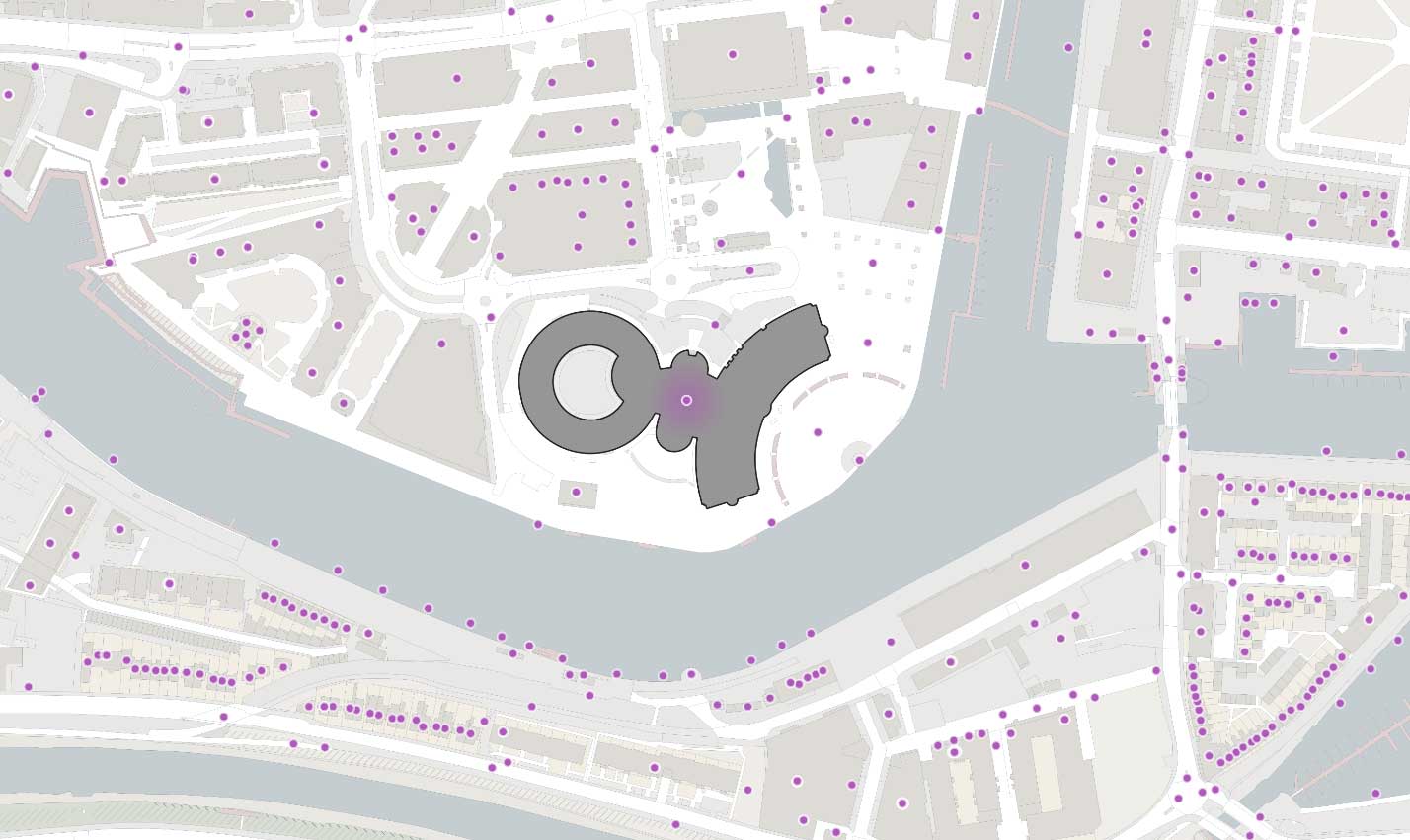
オードナンス・サーベイの地理空間データ処理において、日常的に行われている最も一般的な PIP 結合は、GB 内の全ポイントジオメトリ（約 3,700 万個）と、全ての大規模な建物のポリゴンジオメトリ（約 4,600 万個）との結合です。

隠れたコスト

結合関係の複雑性について考察するなかで、見落としていた点が明らかになりました。従来の複雑性においては、各ペアの解決に固定のコストを想定していたのです。具体的には、結合操作の際に各ペアのレコードに一致するかしないかを確定するためのコストが固定化されていました。これを O(join) とすると、結合の真のコストは、O(n*m)*O(join) になります。従来の同値関係クラスでは、左辺の結合キーが右辺の結合キーと一致するかを評価するだけであるため、O(join) は O(1) とみなせます。簡単に言えば、比較のコストは 1 つの算術演算で求められ、一定になります。ただし、そうでない場合もあります。例えば、文字列比較を行う際の結合は、2 つの整数の等価性を評価する場合よりもコストがかかります。

では、PIP の場合、相対的なコストはどの程度になるでしょうか。PIP を求める際に最も広く使われているアルゴリズムは、レイトレーシング法です。このアルゴリズムの複雑性は O(v) で、v は対象となるポリゴンの頂点の数です。このアルゴリズムは、凸形状にも非凸形状にも適用でき、どちらの場合でも同程度の複雑性が維持されます。

コストモデルに比較コストを加えると、複雑性の合計は立方体になります。O(join) を O(v) に置き換え、v を頂点の平均数とすると、複雑性の合計は O(n*m)*O(v) になります。ただ、これではコストも時間もかかります。

効率的なアプローチ

O(n*m)*O(v) をさらなる改善が可能です。Spark を使用することで、デカルト積の複雑性を解消できます。Spark ではハッシュ結合が利用されており、結合述語に応じて、以下の結合戦略のいずれかを実行できます。

• ブロードキャストハッシュ結合。複雑性：O(max(n,m))*O(join)
• シャッフルハッシュ結合（Grace Hash 結合に類似）。複雑性： O(n+m)*O(join)
• シャッフルソートマージ結合。複雑性：O(n*log(n)+m*log(m))*O(join)
• ブロードキャストネスト化ループ結合（デカルト結合）。複雑性：O(n*m)*O(join)

どうでしょうか。Spark を使えば、最もコストのかかる結果を避けられるように思えます。しかしながら、PIP 結合では、Spark のデフォルトは、デカルト結合になります。その理由は、PIP が従来の同値ベースの結合とは異なり、一般的な関係に基づいているからです。これらの結合はシータ結合クラスとして知られていますが、通常は実行の難易度が高く、エンドユーザーによるシステムの設定が必要になります。このように、導入時点での負担はありますが、望ましいパフォーマンスを得ることは可能です。

空間グリッドインデックス（疑似同値としての PIP）

厳密にいえば、PIP を同値関係にするアプローチはありません。ただし、空間グリッドインデックスの手法を活用すれば、PIP の効率を実質的に同値関係に近づけることは可能です。

空間グリッドインデックスでは、座標空間内で互いに近接するジオメトリを論理的にグループ化することで、効率的に座標空間のインデックスを作成できます。これは、座標系内のポイントをインデックス ID に一意に関連付けることで実現されており、参照空間の精度や解像度を異なるレベルで表現することが可能になります。また、この地理空間グリッドインデックスシステムは階層的なシステムとなっており、表現レベルが異なる場合でも、インデックス間に明確な親子関係が存在します。

これにより、各ジオメトリに、そのジオメトリが属するインデックスを割り当てると、インデックス ID 間の同値関係を同値関係のプロキシとして使用できるようになります。PIP（またはその他のジオメトリベースの関係処理）を実行する際には、同じインデックスに属するジオメトリに対してのみ行います。

ここで重要な点は、POINT ジオメトリは 1 つのインデックスにしか属しませんが、LINESTRING や POLYGON などの他のジオメトリタイプは、複数のインデックスにまたがる可能性があるということです。すなわち、インデックス空間を介して PIP 関係を解決するためのコストは O(k)*O(v) になります。k はジオメトリの表現に使用されるインデックスの数、v はそれらのジオメトリの頂点の数です。複雑なジオメトリのレコードを、同じジオメトリを持つ複数のインデックスレコードに展開することで、比較時の値を高めているわけです。

こうするのが望ましい理由は、1 組のジオメトリを比較する際の値を高める一方で、大規模な地理空間結合を行う際に常に問題となる完全なデカルト積を避けることができるからです。後で詳しく説明しますが、インデックス ID 間での結合で、不要な比較を大幅に省略できます。

また、複雑なジオメトリを含むデータソースは、この手法に用いられるデータソースに比べ変化が少ないこともあります。通常、複雑なジオメトリは、地域、特定の領域、建物などを表しており、これらは時系列における変動が少ない概念です。時間の経過とともに変化するオブジェクトはほとんどなく、変化があったとしてもわずかです。つまり、複雑なジオメトリの前処理に時間がかかるとしても、ほとんどのジオメトリでこの処理は 1 回限りで済みます。このアプローチは、頻繁に更新されるデータにも適用可能です。インデックス ID 間の関係で結合を行う際に省略できるデータ量は、1 つのジオメトリ表現に使用される行数の増加分を上回ります。

BNG インデックスシステム

BNG は、1936 年に制定されたローカル座標リファレンスシステム（CRS：Coordinate Reference System、EPSG:27700）で、グレートブリテン島をカバーする全国地図用に設計されました。グローバル CRS とは異なり、グレートブリテン島の地形に沿った形状をしており、シリー諸島の南西を原点（0, 0）として正方形の格子上に座標が配置されています。

グリッド境界内では、地理的グリッド参照（またはインデックス）を使用して、メートル単位で表される異なる解像度のグリッドスクエアを特定します。BNG の東方座標（x）および北方座標（y）との変換も可能です。グリッドの原点の位置からすると、東方座標と北方座標は常に正の値になります。BNG は、オードナンス・サーベイが全国的に行っている地図作成業務で取得した全位置情報データの主要基準系として使用されており、グレートブリテン島で オードナンス・サーベイのデータを使用する公共ユーザーや民間ユーザーに広く採用されています。

各グリッドスクエアを、各辺の長さがグリッド参照の解像度に等しいポリゴンジオメトリとして表現することが可能です。そのため、地理空間データの分割戦略の起点としてBNG は非常に使いやすいものとなっています。正方形を構成要素とすることで、手法の汎用性を損なうことなく、最初に検討すべき事項の多くをシンプルにできます。

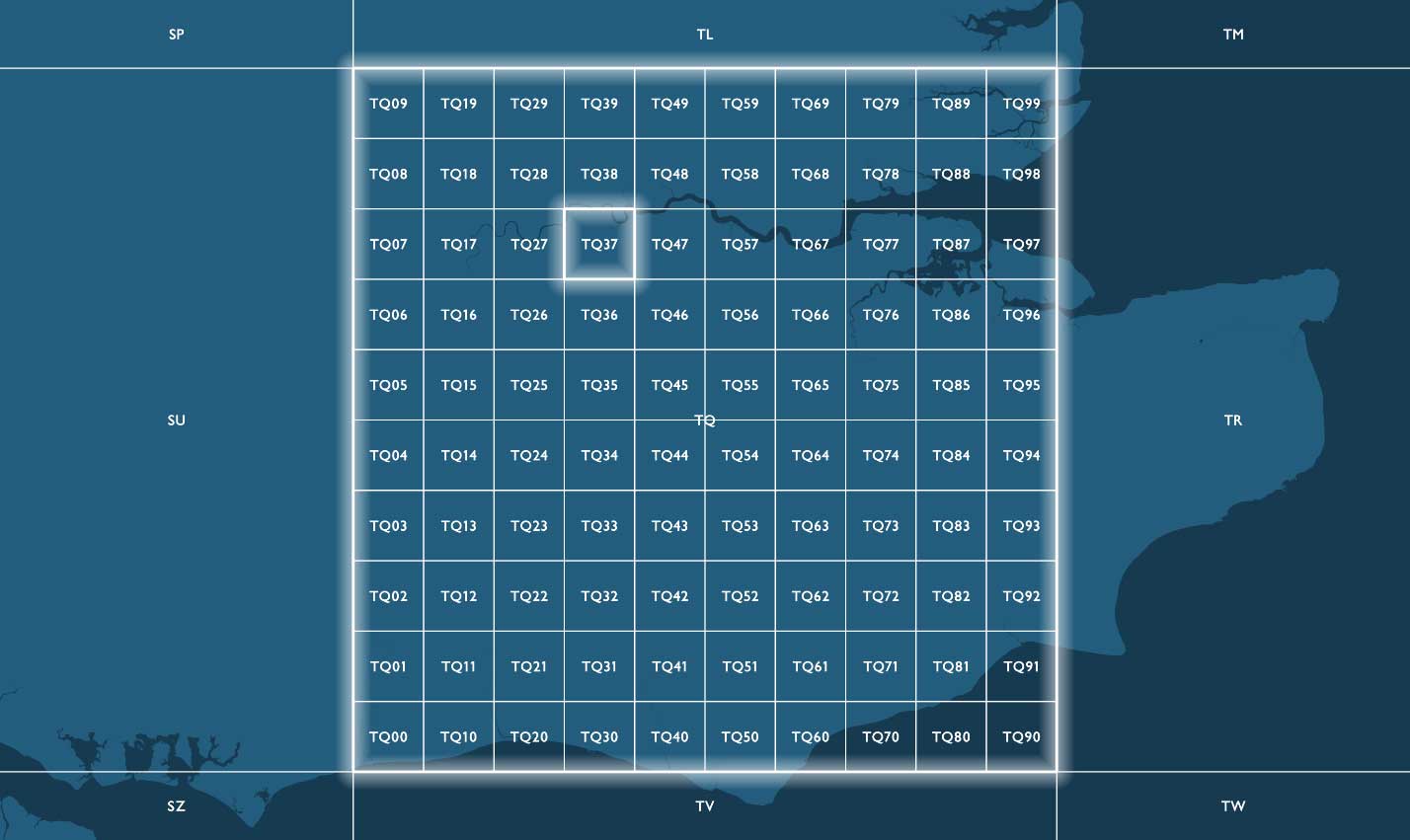
慣例的に、BNG のグリッド参照は、複数の文字と特定の解像度で示されたグリッドスクエアの南西の隅の座標から成る文字列で表現されます。参照の最初の 2 文字は、100,000m（100km）の長さを持つ 91 個のグリッドスクエアの 1 つを示す文字（プレフィックス）で、TQ などになります。100km四方のグリッドスクエア 91 個のうち、グレートブリテン島の地形をカバーしているのは 55 個で、残りの部分は英国の海域です。

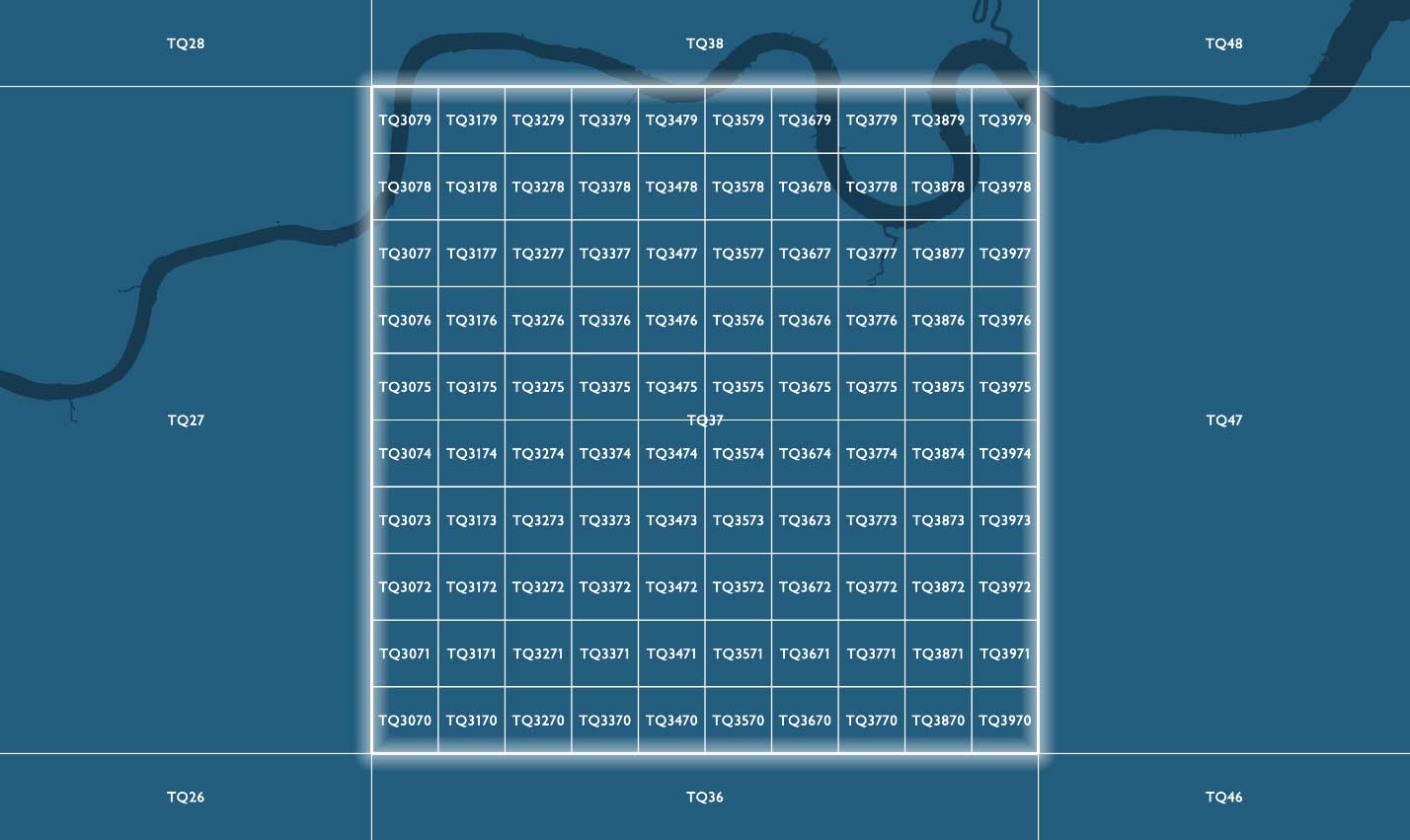
100km 以下の詳細なグリッド解像度で識別される参照では、2 文字の後に、親グリッドスクエア階層内の子グリッドスクエアを示す x および y の整数値が追加されます。子グリッドスクエアには、左下（南西）の隅から東方（x）および北方（y）に向けて 0〜9 の番号が振られています。

BNG を選択した理由

今回検討したグローバルインデックスシステムは他にもありますが、BNG を選んだ理由は以下のとおりです。

• BNG システムは、オードナンス・サーベイの地理空間データコレクションを元にしており、ほぼ全てのデータが BNG CRS（EPSG:27700）で参照されています。このデータには、オードナンス・サーベイの航空写真タイルや、デジタル地形モデル（DTM）やデジタルサーフェスモデル（DSM）などのラスターデータが含まれます。
• BNG を使用することで、深層学習アプリケーションのトレーニングパッチを導出するためのラスターデータのクリッピングやマスキングなど、分析用ベクターデータやラスターデータの効率的な検索とコロケーションが可能になります。
• BNG の使用により、世界測地系 1984（WGS-84）（EPSG:4326）や欧州地球基準座標系 1989（ETRS89）（EPSG:4258）の CRS へ変換する負担を OSTN153 変換グリッドを経由して、回避することができます。CRS が異なると地球モデルが異なるパラメーターで作成されることになり、WGS84 などのグローバルシステムと BNG などのローカルシステムとの比較に際してオフセットが発生します。衛星座標と BNG 座標間で正確な変換を行うために、オードナンス・サーベイでは、約 175 万個のパラメーターを含む15MB の補正ファイル OSTN15 を公開しています。

オードナンス・サーベイが担当しているのはグレートブリテン島という地域であることから、BNG を選択するのが最も合理的です。対象がよりグローバルな場合は、より適切な選択肢として H3 や S2 を検討するべきでしょう。

空間分割戦略としての BNG

空間分割戦略とは、地理空間データを重複がない領域に分割するためのアプローチを定義するものです。今回は、グレートブリテン島の各地域が、異なる解像度の BNG グリッドスクウェアで重複しないように表現されています。各ジオメトリをカバーする BNG インデックスを取得することで、インデックス属性を結合キーとして使用します。そして、複数の行を結びつけることで、結びつけられた行の中でのみ空間述語をテストすることができます（例：ジオメトリ A とジオメトリ B が交差しているか、ジオメトリ A がジオメトリ B を含むかなど）。

これは非常に重要なことです。元のデータを地理空間的に結びつけられた部分データに分割することで、驚くほど簡便な並列処理になり、Spark や PySpark に非常に適したものとなります。別々の部分データを異なるマシンに送信し、相互に結合される可能性の高いデータのローカル部分を比較できます。ロンドンの建物にマンチェスターの住所が含まれているかどうかを調べてもあまり意味がありません。地理空間インデックスを使用することで、このような直感的な判別処理が可能になります。

ベースライン

今回のソリューションは、Python と PySpark を使って実現しています。オードナンス・サーベイからは、東方座標と北方座標のペアを一意の BNG インデックス ID に変換するロジックが提供されました。そして、出力の偏りが生じないように、ポイントおよびポリゴンについてランダムなデータセットを使用しました。グレートブリテン島の領域全体に、1000 万個のポイントと100 万個のポリゴンを同じ方法で散在させています。このようなポリゴンデータを生成するために、GeoJSON セットを Spark のデータフレームに読み込み、ランダム関数とジェネレータ関数（explode）を併用して偏りのないデータセットを生成しました。データには乱数性が導入されているため、ポイントとポリゴンの関係は多対多であることが想定されます。

検討に用いたベースラインアルゴリズムは自然結合で、通常は最適化されていないシータ結合になると考えられます。このアプローチは、実行時にはブロードキャストネスト化ループ結合として評価されます。

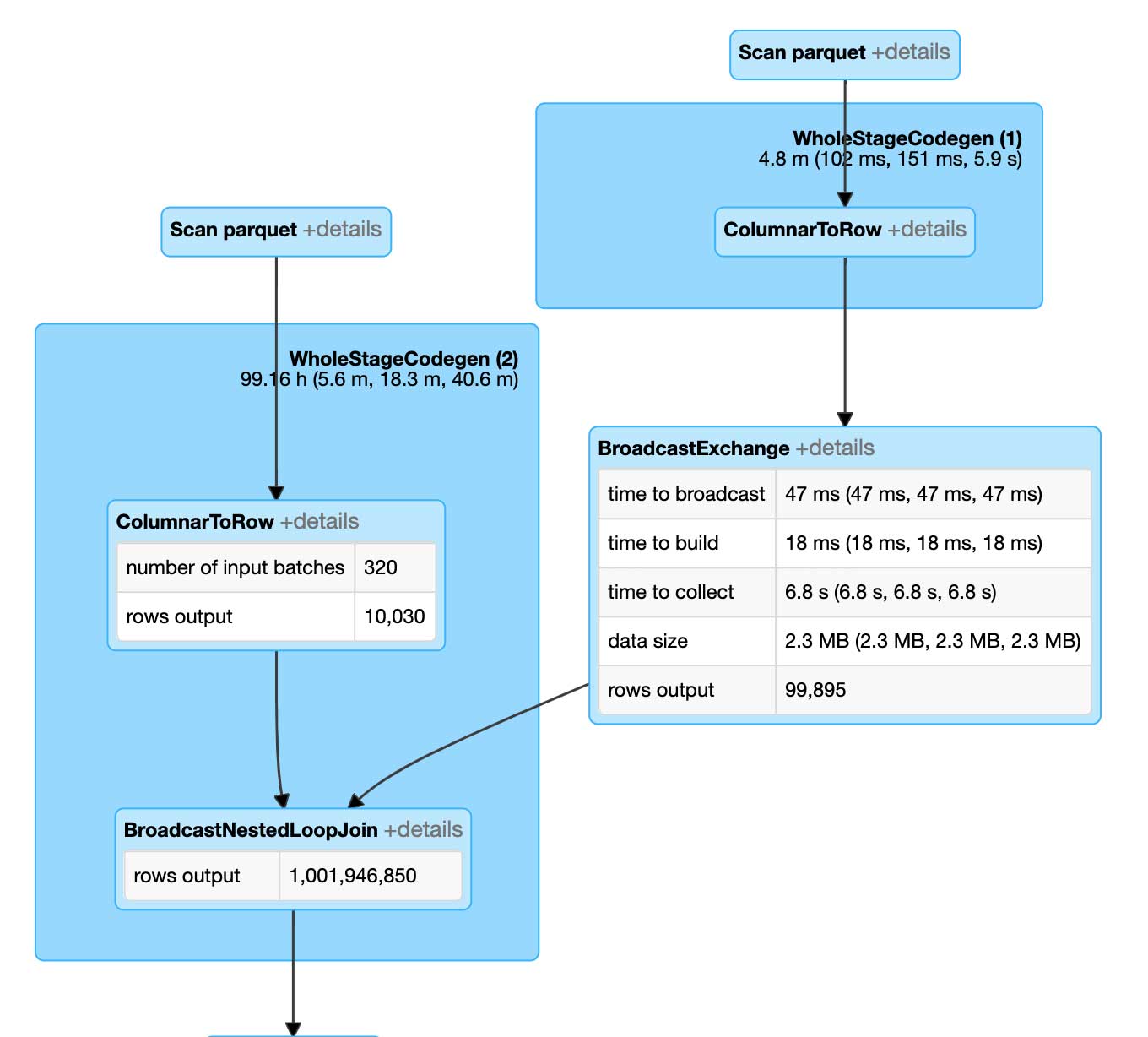
ブロードキャストネスト化ループ結合の実行には非常に時間がかかります。デカルト積と同様に評価されるためです。ポイントとポリゴンの各ペアが、PIP 関係に対して結合の解決前に評価されます。その結果、10 万個のポイントを 1 万個のポリゴンに結合するためには、10 億回の比較が必要となります。なお、これらのデータセットはいずれもビッグデータと呼称するほどのサイズではありません。

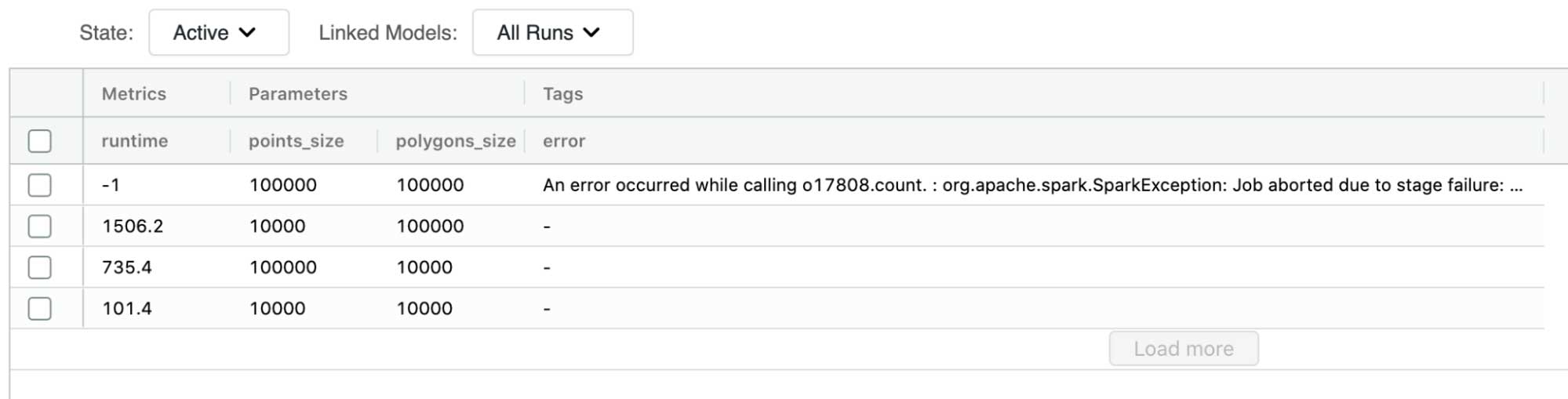
MLflow を使用して一連の自然結合を実行し、改善を見込むベースラインのパフォーマンスを評価したところ、自然結合の場合で、1 万個のポイントと 10 万個のポリゴンの結合が最大の成功例でした。データ量がこれ以上に増えると、Spark ジョブが失敗し、期待どおりの出力が得られませんでした。この失敗の原因は、実行しようとしていたワークロードが最適化されていなかったことです。

問題の整理 

ジオメトリの形状に関わらず、全てのジオメトリを BNG に沿ったバウンディングボックスで表現できないでしょうか？元のジオメトリの全体をバウンディングボックス（長方形のポリゴン）の範囲内に収め、一定の解像度で同じ領域をカバーする BNG インデックスとして表現するということです。

そうすれば、最適化されたシータ結合でのみ結合が行われるようになります。PIP 関係でポイントがポリゴンの内側にあるか判定する際に、ポリゴンの表現に使用される BNG インデックスのいずれかに該当する場合にだけ判定が行われるわけです。これにより、結合のコストが数桁分の単位で削減されます。

この BNG インデックスは、以下のコードを使用して生成しました。なお、このブログでは、bng_to_geom、coords_to_bng、bng_get_resolution の各関数については解説していません。

このコードにより、コストの少ない方法であらゆる形状を表現できます。表現対象から外れるものが出ることを防ぐため、BNG インデックスの候補と元のジオメトリの間には交差関係を使用しています。なお、より効率的な実装として包含関係と図心を利用するアプローチもありますが、偽陽性と偽陰性を許容できない場合は有効ではありません。BNG インデックス ID からジオメトリ表現を生成する bng_to_geom 関数、BNG インデックス ID から選択された解像度を判別する bng_get_resolution 関数、座標から BNG インデックス ID を返す coords_to_bng 関数が用意されているものと考えてください。

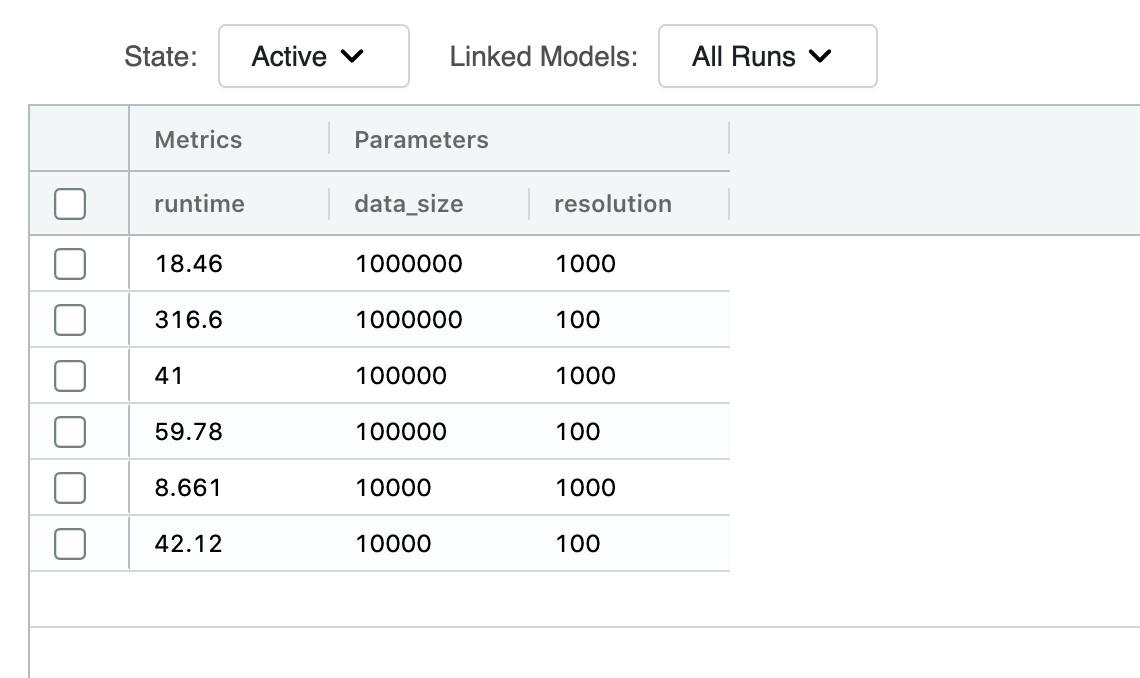
ポリゴンによるバウンディングボックス表現を、BNG インデックスシステムで解像度とデータセットサイズを変えて実行しました。解像度が 100 以下の場合、処理は失敗します。また、出力における解像度の単位はメートルです。解像度が 100m 以下の場合に失敗するのは、表現の処理が過重になってしまうためです。ポリゴンの形状は不揃いであるため、それぞれの大きさは一定ではありません。あるポリゴンは十数個のインデックスで表現されますが、他のポリゴンは数千個のインデックスで表現されます。つまり、データを生成する Sparkジョブのパーティション間で、必要なコンピューティングリソースとメモリ使用量に大きく差異が生じることになります。

今回、ポイントデータセットの変換についてはベンチマークを省略しています。行の追加が発生せず、列が 1 つ追加されるだけの比較的単純な処理であり、解像度の違いが実行時間に影響を及ぼすことはないためです。

これで、結合の両辺が対応する BNG で表現されました。あとは調整した結合ロジックを実行するだけです。

このようにコードを修正した結果、Spark の実行プランが変わりました。Spark で、最初に BNG インデックス ID に基づいてソートマージ結合を実行し、比較の総数を大幅に減らすことができるようになりました。さらに、各ペアの比較は PIP 関係よりもはるかに短い文字列同士の比較です。この最初の段階で、全ての結合セットの候補が生成されます。その後、この候補のセットに対して PIP 関係のテストを行い、最終的な出力を決定します。このアプローチにより、PIP 演算を実行する回数を確実に抑えることが可能です。

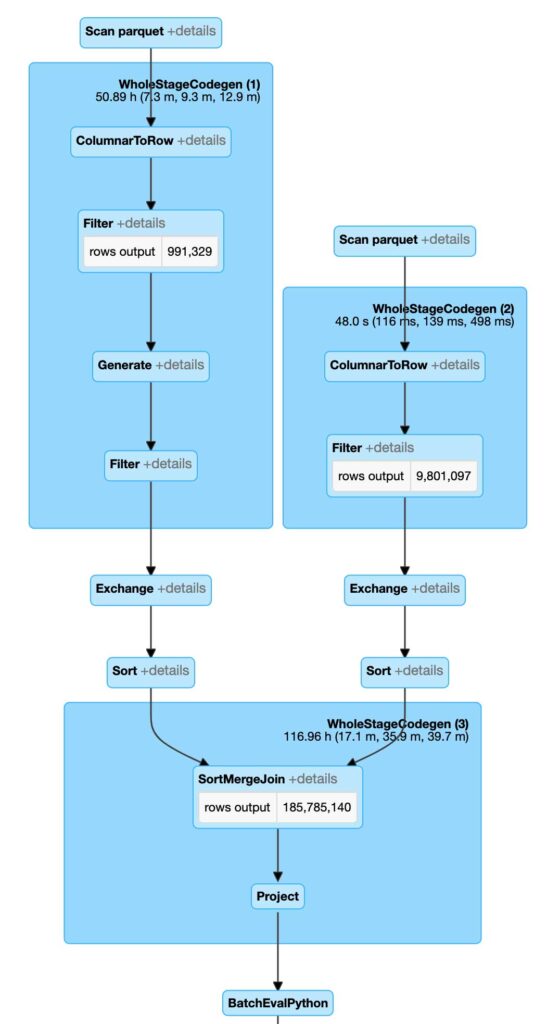
実行プランを見ると、Spark では従来のアプローチと全く異なる処理の行われていることがわかります。最も注目すべき点は、Spark でブロードキャストネスト化ループ結合の代わりにソートマージ結合が実行されていることで、これにより効率性が大きく向上しています。実行される PIP 操作が 10 億回から 1 億 8600 万回になり、これだけでも大量の結合を実行する際のレスポンスが改善され、元のアプローチに見られる大きな失敗を回避できます。

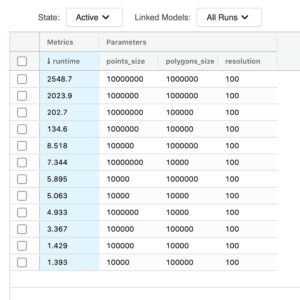
このシンプルで効果的な最適化により、1,000 万個のポイントと100 万個のポリゴンの PIP 結合を約 2,500 秒で実行できるようになりました。ベースラインと比較すると、実行できた最大の処理が 1 万個のポイントと 10 万個のポリゴンの結合で、その規模の結合でさえ同じハードウェア上で約 1500 秒を要しています。

分割統治法

100 万行の規模のデータセット間で結合が実行できるのは素晴らしいことです。しかし、最も大きなベンチマークで結合処理に約 45 分（2500 秒）かかっています。膨大な地理空間データに対してアドホックな分析（解析）を行いたい場合、これでは時間がかかり過ぎです。

このアプローチをさらに最適化する必要があります。最適化の 1 つ目の候補は、バウンディングボックスの表現です。ポリゴンをバウンディングボックスで表現すると、偽陽性のインデックスなど、元のジオメトリと全く重ならないインデックスが多く含まれてしまいます。

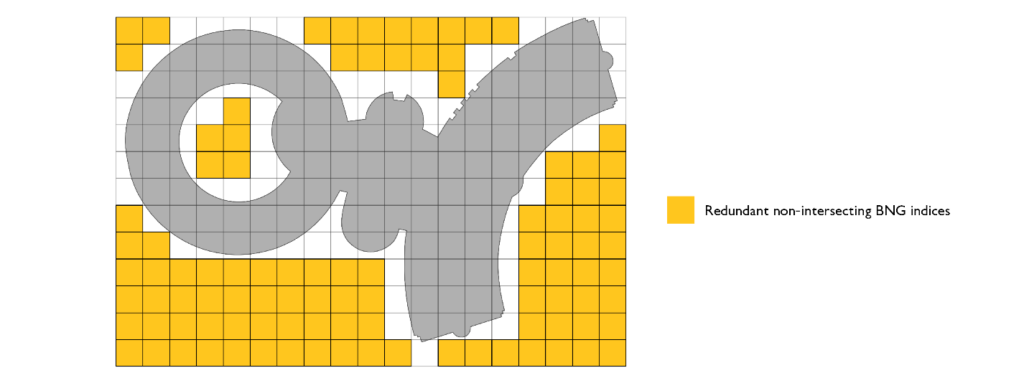
この点に該当するコードを最適化するには、元のジオメトリに対してポリフィルメソッドで intersects 関数呼び出しを使用します。

この最適化では、intersects 呼び出しを使用することでコストが増加しますが、結果的にインデックスセットが少なくなり結合の対象面が小さくなるため、処理速度が向上します。

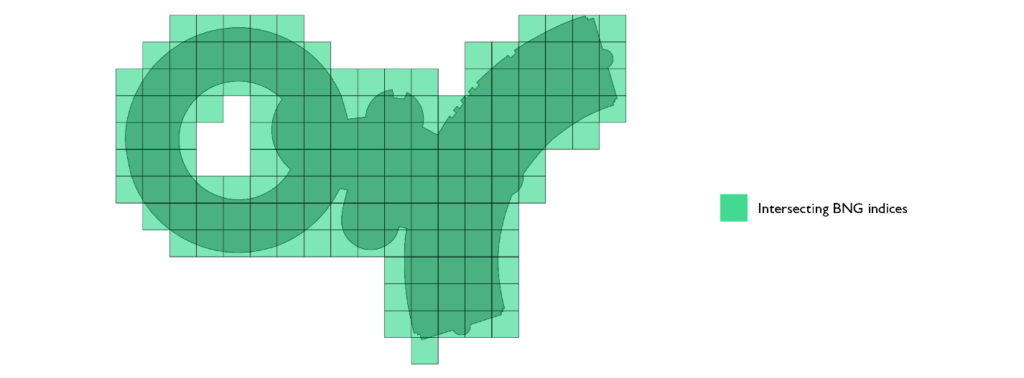
次の最適化は、2 つのインデックスセットに分割して表現することです。この表現では、全てのインデックスが同じではありません。ポリゴンの境界に接しているインデックスには、インデックス同士の結合後に PIP フィルタリングが必要です。ポリゴン表現内に属していて境界に接していないインデックスであれば、追加のフィルタリングは不要です。さらにポリゴン内に属していることが確実なインデックスについては、PIP の処理を省略できます。

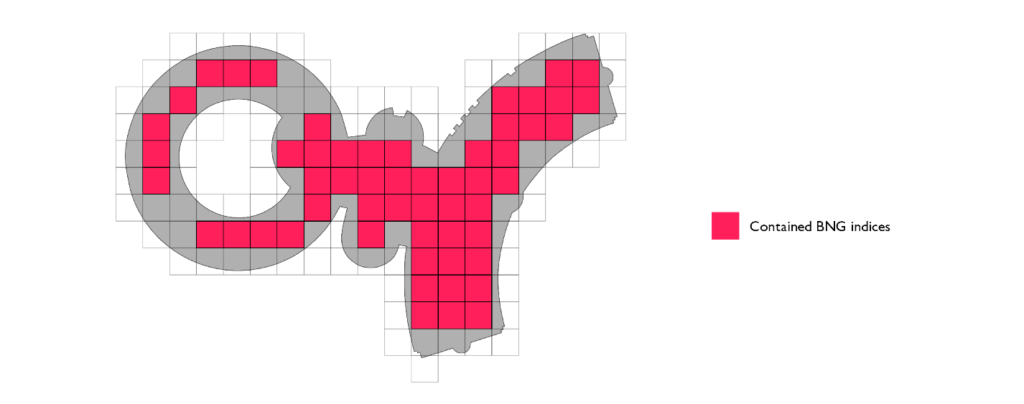
最後の最適化は、モザイク法です。ポリゴンの境界に接するインデックスセット（境界セット）に属する各インデックスに、元のジオメトリ全体を関連付けるのではなく、対象となる部分だけをトラッキングします。対象のインデックスを表すジオメトリとポリゴンを交差させると、ポリゴンのローカル表現が得られます。つまり、元のポリゴンのうち、対象のインデックス領域に関連する部分です。今回はこれを「ポリゴンチップ」と呼称することにしました。

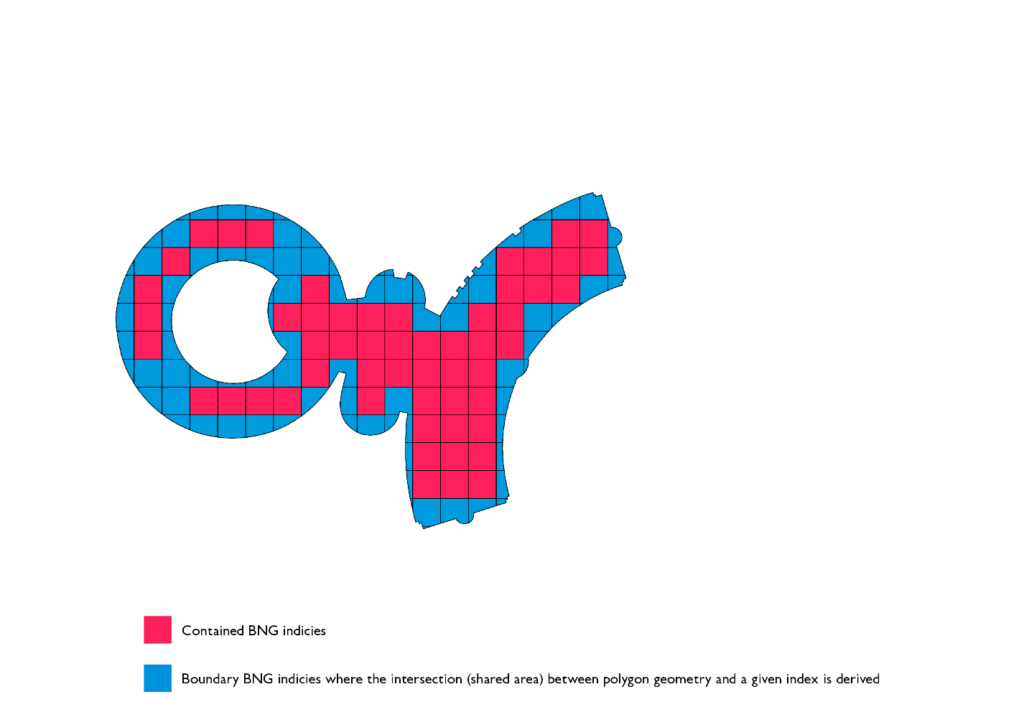
ポリゴンチップには、最適化の面で 2 つの利点があります。1 つは、インデックス間結合の実行後に生じる PIP フィルターの効率が大幅に改善することです。これは、レイトレーシングアルゴリズムが O(v) の複雑さで実行され、個々のポリゴンチップの頂点数が元のジオメトリよりも平均して 1 桁少ないことから可能になります。もう 1 つは、ポリゴンチップによる表現は元のジオメトリよりもはるかに小さいことから、ソートマージ結合ステージのシャッフルステージの一部として、非常に少ないデータのシャッフルが実現することです。

これらを全てまとめると、以下のようなコードになります。

このコードは、元のバウンディングボックスの方法とよく似ています。一部のコードの重複を避けるため、いくつかの軽微な変更を行って add_children ヘルパーメソッドを別に用意しました。

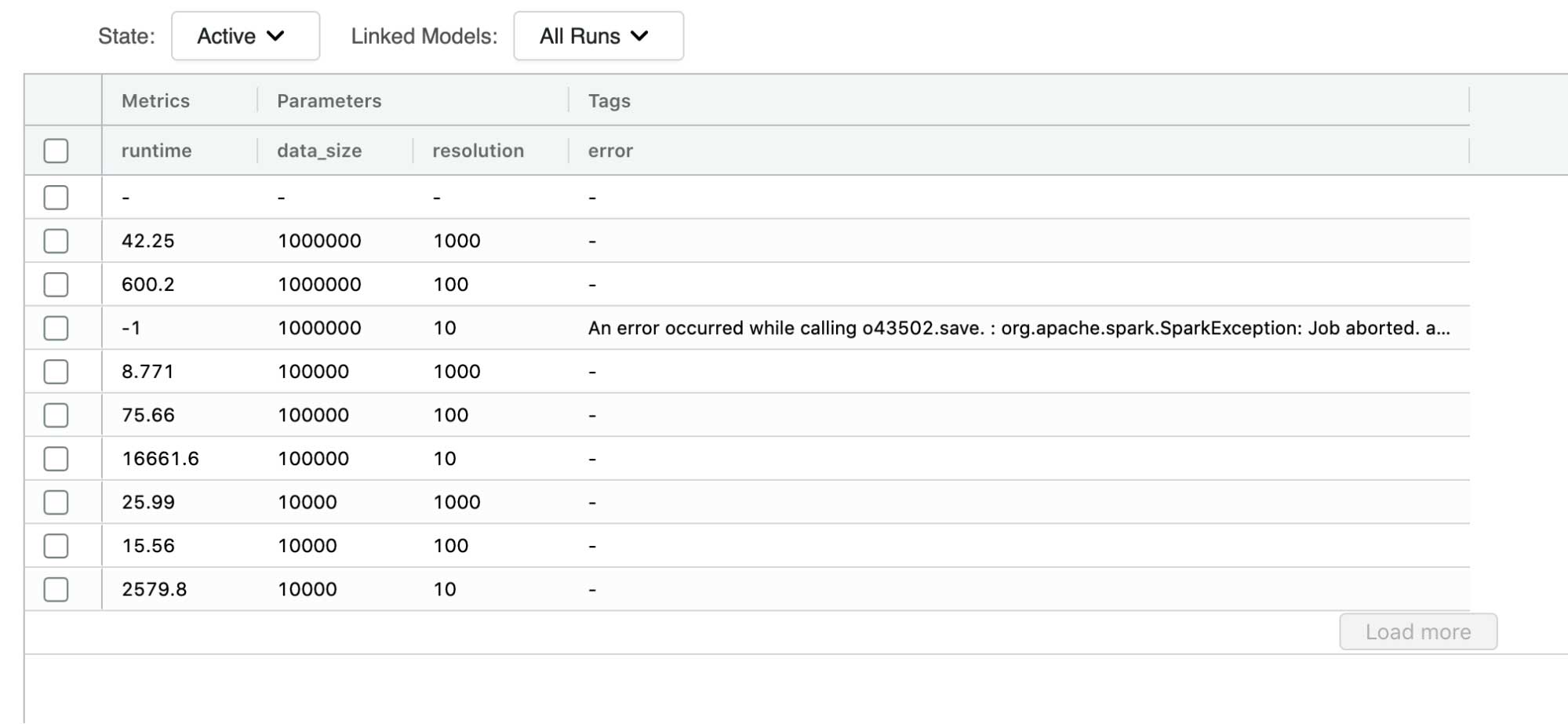
ポリゴンをバウンディングボックスで表現したときと同様に、データ生成のベンチマークを行いました。バウンディングボックスの方法と共通していたのは、100m 以下の解像度ではポリゴンの表現が過重になってしまうことです。ポリゴンチップの方法では 10m の解像度で最大 10 万個のポリゴンデータを生成できましたが、この場合でも本番運用のワークロードとしてはデータ生成時間が長すぎます。

100m の解像度では非常に有望な結果が得られました。100 万個のポリゴンのデータセットを生成して書き出すのにかかった時間は約 600 秒です。バウンディングボックスの方法では約 300 秒で手順もシンプルですが、データの準備段階でいくらかの処理時間が加わります。ポリゴンチップの方法も検討に値するのではないでしょうか？

モザイク法の有効性（高速性）

モザイクデータを用いた PIP 結合についても同様のベンチマークを実施しました。境界セットとコアセットのインデックスが正しく最も効率的な方法で利用されていることを確認するため、結合ロジックを少し変更しています。

is_dirty 列は、ポリフィルメソッドで導入しています。元のジオメトリの境界と接しているインデックスに、dirty のマークが付けられます（is_dirty=Trueに設定）。これらのインデックスに該当するポイントが比較対象のジオメトリの範囲内に含まれているかを正しく判別するには、事後のフィルタリングが必要になります。is_dirty のフィルタリングを pip_fiter の呼び出しの前に行うことが非常に重要です。Spark の論理演算子には短絡評価の機能があり、論理式の最初の部分が true の場合、2 番目の部分は実行されません。

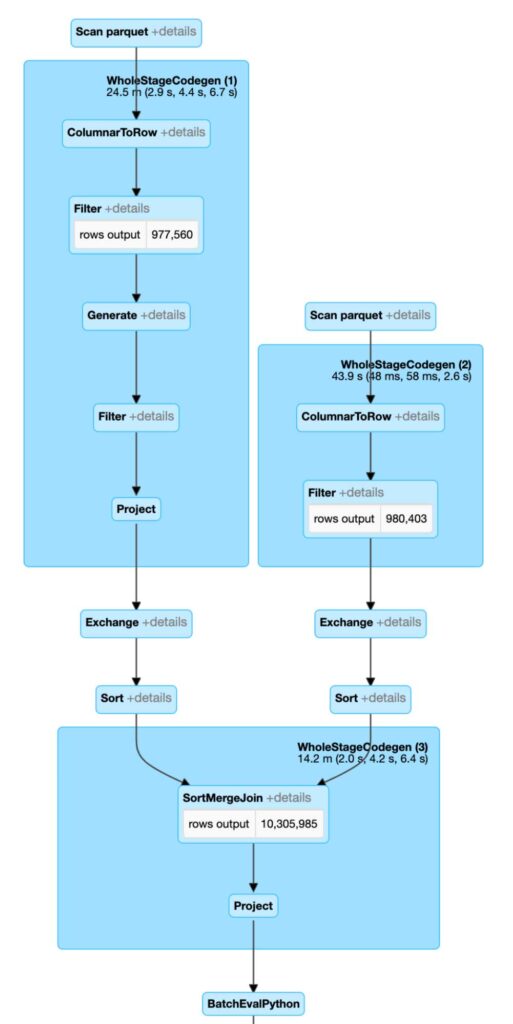
このコードにより、Spark での実行プランがより効率的になります。インデックス空間での表現が改善されたことで、結合面が非常に小さくなりました。また、インデックスセットの分割表現とジオメトリのモザイク分割により、事後フィルタリングの有効性が高まりました。

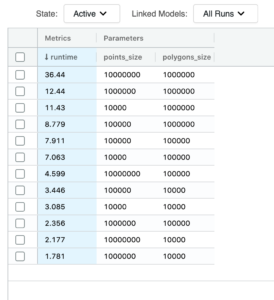
これで、今回の取り組みを数値化することができました。1,000 万個のポイントと 100 万個のポリゴンの PIP 結合は、今回考案されたモザイク法であれば、37 秒で実行されます。それに対し、バウンディングボックス方式では、同様の結合を同じインデックス解像度で行った場合、2,549 秒になります。つまり、実行時間が 69 分の 1 に短縮されています。

この数値は、純粋な実行時間だけを対象としたものです。準備時間がモザイク法で 600 秒、バウンディングボックス方式で 317 秒あるため、それらを含めた合計時間で考えると、パフォーマンスの改善は 4.5 倍になります。

なお、これらの改善の程度は、ジオメトリデータの更新頻度と照会頻度に応じて、大きく変わる可能性があります。

一般的なアプローチ

今回の記事では、BNG（British National Grid）を参照インデックスシステムとして使用する） PIP（Point in Polygon）結合について取り上げました。しかし、今回の手法はより汎用的なものです。他の階層的な地理空間システムにも、同じ最適化のアプローチが適用できます。異なる点は、ポリゴンチップの形状と利用できる解像度です。また、大量のポリゴンの交差結合など、2 つの複雑なジオメトリ間でのシータ結合の規模拡大にも有効です。

今回の取り組みにおいては、PySpark の利用を優先し、サードパーティのフレームワークの導入は避けました。そうすることで、データブリックスのソリューションが利用しやすくなり、主に Python ユーザーを対象にカスタマイズ可能であると考えています。

このソリューションでは、いくつかの独創的な最適化を行うことで、ジオメトリ前処理の負担を最小限に抑えつつ、バウンディングボックス方式に比べて最大 70 倍の性能向上を実現できることが確認されました。

また、大規模な PIP 結合の実行時間を数秒単位の時間に抑えることに成功し、そのようなデータを利用したアドホックな分析が可能になることを示しました。