Check our Solution Accelerator for Matrix Factorization for more details and to download the notebooks.
Recommenders are a critical part of the modern retail experience. Online shoppers rely on recommendation engines to navigate huge portfolios of available products. Marketers leverage recommenders to prioritize the items presented in banner ads and email marketing campaigns. And in omnichannel scenarios, recommenders are increasingly being used to bring personalized product suggestions to in-store shoppers and to assist order fulfillment personnel with product substitutions.
When done right, recommendation engines can create the kinds of personalized experiences consumers increasingly expect from retail outlets. Successful use of these capabilities not only increases customer preference for a given channel, but they can increase the frequency and amount of spend, strengthening a retailer's bottom line.
But simply plugging-in any ol' recommender isn't likely to lead to success. Instead, it's important to understand that different recommenders provide different kinds of recommendations, some of which are more appropriate at certain points in the customer journey than in others. For this reason, it's important to carefully consider the context within which a recommendation is being made and tailor your choice of recommendation strategies and supporting engines to that specific scenario.
A quick search for recommendation engines is likely to bring back a large (and growing) number of suggested algorithms. With each new competition or white paper on the topic of recommenders, there seems to be a new algorithmic approach that grabs the attention of the developer community.
New algorithms are often exciting for their ability to scale, deal with a difficult edge case or deliver a slightly better evaluation metric score relative to another frequently employed algorithm. They also tend to be significantly more complex than their predecessors. Without significant familiarity with recommenders in general and the specific libraries used to implement them, it can be very difficult for developers to recognize the appropriateness of an approach for a given business context and navigate the decision points that affect the ability of these solutions to deliver the desired results.
For organizations getting started with recommenders, we suggest deciding if a given touchpoint calls for recommendations of similar items or items suggested by the user's activity. If what is needed is the former, a content-based recommender which compares items for similarities along different dimensions is required. If what is needed is the latter, a collaborative filter is the appropriate choice.
Collaborative filters have a long history and come in many different flavors. If you've encountered recommendations presented as products we think you'd like, based on your purchase history, or people like you also bought, you've encountered collaborative filtering. These recommenders leverage customer preferences as expressed through explicit ratings or implied ratings suggested through patterns of engagement to understand which products a particular customer is likely to find appealing. One of the most basic but still quite powerful of these is a matrix factorization recommender.
The matrix factorization recommender considers the intersection of all users and products. If we envision this intersection as a matrix with preferences (ratings) associated with the products a given user has actually engaged, we are typically left with a large, sparsely populated structure (Figure 1).
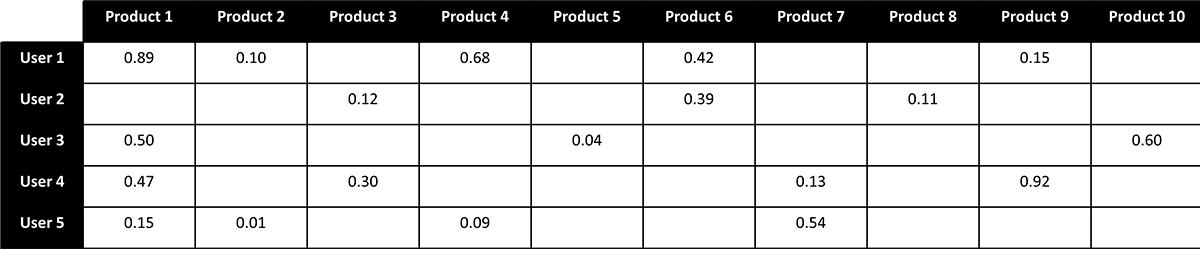
Our goal is to examine the available ratings to derive a relatively small set of values (often referred to as latent factors) that capture the relationships between these ratings. The mathematics behind how this is done can be a bit complex but the underlying idea is that we can decompose (factorize) the large, sparsely populated user-product matrix into two dense and much smaller matrices that would allow us to recreate the provided ratings (Figure 2).
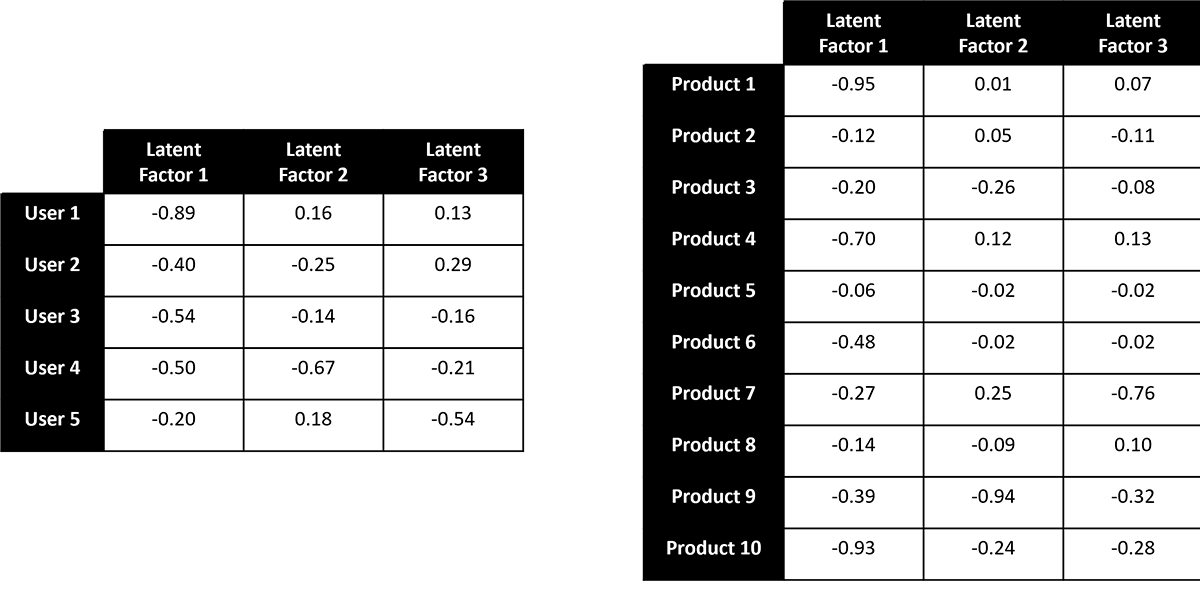
The smaller submatrices provide a nice, compact way to capture the patterns in our original matrix. They also have the side-effect of allowing us to infer user preferences for products a user has not yet engaged (Figure 3). Again, the math can be a bit complex, but intuitively the idea is that the degree to which different users share a preference for an overlapping set of products can be used to infer preferences for the products where there has not been overlapping consumption.
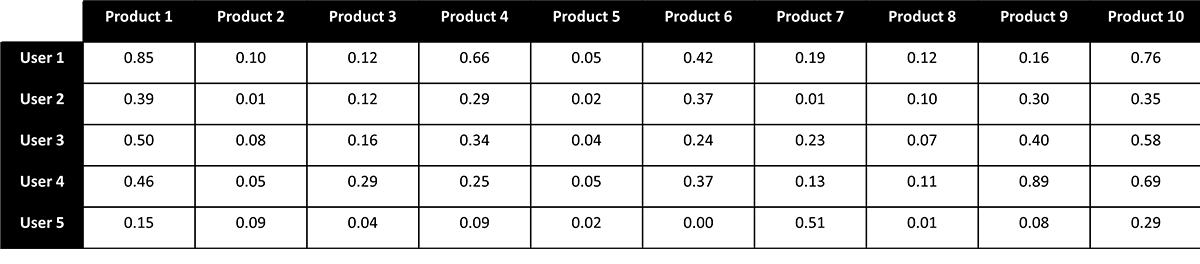
Apache Spark™ provides a scalable implementation of matrix factorization
Matrix factorization was first popularized in the late 2000s with the pursuit of the Netflix prize and is still widely used today given its relative simplicity and robustness. Several founding members of the Apache Spark community were involved in the Netflix prize competition so it should come as no surprise that matrix factorization has found its way into the Spark ecosystem.
The specific implementation of matrix factorization within Apache Spark is referred to as the Alternating Least Squares (ALS) algorithm. ALS implements matrix factorization iteratively by optimizing one of either of the two submatrices (Figure 2) while holding the other steady in a back and forth motion until the matrices arrive at a stable answer or the maximum number of iterations is exhausted.
While the ALS algorithm does not require the use of a distributed platform such as Spark, it can benefit from it by subdividing the user and product submatrices into associated subsets of users and items (blocks) organized in such a way that the information exchanged between blocks with each iteration is limited. This allows the blocks to be distributed across a Spark cluster, scaling out the processing of the algorithm and reducing the elapsed time required for the model to converge. For real world datasets where the number of users multiplied by the number of available products can quickly jump into the trillions of combinations, scalability is essential making the Spark implementation of ALS an ideal choice for this type of recommender.
We have provided a demonstration to help you get started
To demonstrate how to develop a matrix factorization recommender using the Spark MLLib Alternating Least Squares (ALS) algorithm, we've developed a solution accelerator around the Instacart dataset. The Instacart dataset consists of over 200K users and nearly 50K products which produces a matrix of over 10B user-item combinations. This matrix is large enough to choke simplistic implementations of the ALS algorithm (and most matrix factorization algorithms in general) while still being relatively small compared to the matrices that would be associated with most real-world retail scenarios.
In the notebooks, we spend quite a bit of time diving into how we might calculate ratings for items that are not explicitly rated by users and the implications for this in how we approach the development of our recommender solution. We also examine common deployment patterns that enable organizations to integrate the ALS-generated recommendations into user experiences. Please take a look at our Solution Accelerator for Matrix Factorization.
