Fast PEFT Serving at Scale

Building a lightning-fast inference runtime isn't just about raw speed—it's about solving the right problems for real customers. At Databricks, our focus on Data Intelligence means helping customers turn their proprietary data into AI agents that serve production workloads at massive scale. The inference engine sits at the heart of this challenge, orchestrating everything from scheduling of requests to GPU kernel execution. Over the past year, we've built a custom inference engine that both out-performs open source on our customer workloads by 2x in some cases, but also fewer errors on common benchmarks.

With our focus on data intelligence, building AI that can reason over your enterprise data, one of the most critical workloads is serving fine-tuned models, which are either trained by the customer themselves or produced by Agent Bricks. However, full parameter fine-tuned models don’t scale economically when you’re dealing with fragmented requests across dozens of specialized use cases. Finetuning techniques like Low Rank Adapters (LoRA) from (Hu et al, 2021) are popular approaches, as they are memory efficient to fine-tune, and can also keep costs manageable. Work from both our Mosaic AI Research team (Biderman et al, 2024) and the community (Schulman et al, 2025) have established that as a training technique, PEFT has advantageous characteristics.

The challenge we address here, however, is how to make PEFT inference work at scale without sacrificing performance or model quality.

Our World-Class Inference Runtime

Our Model Serving product powers massive amounts of both real-time and batch data at Databricks, and we’ve found that delivering performance on customer workloads means innovating beyond what is available in open-source. That’s why we’ve built a proprietary inference runtime and surrounding system that significantly outperforms the open source alternatives by up to 1.8x in some cases, even just running base models. 

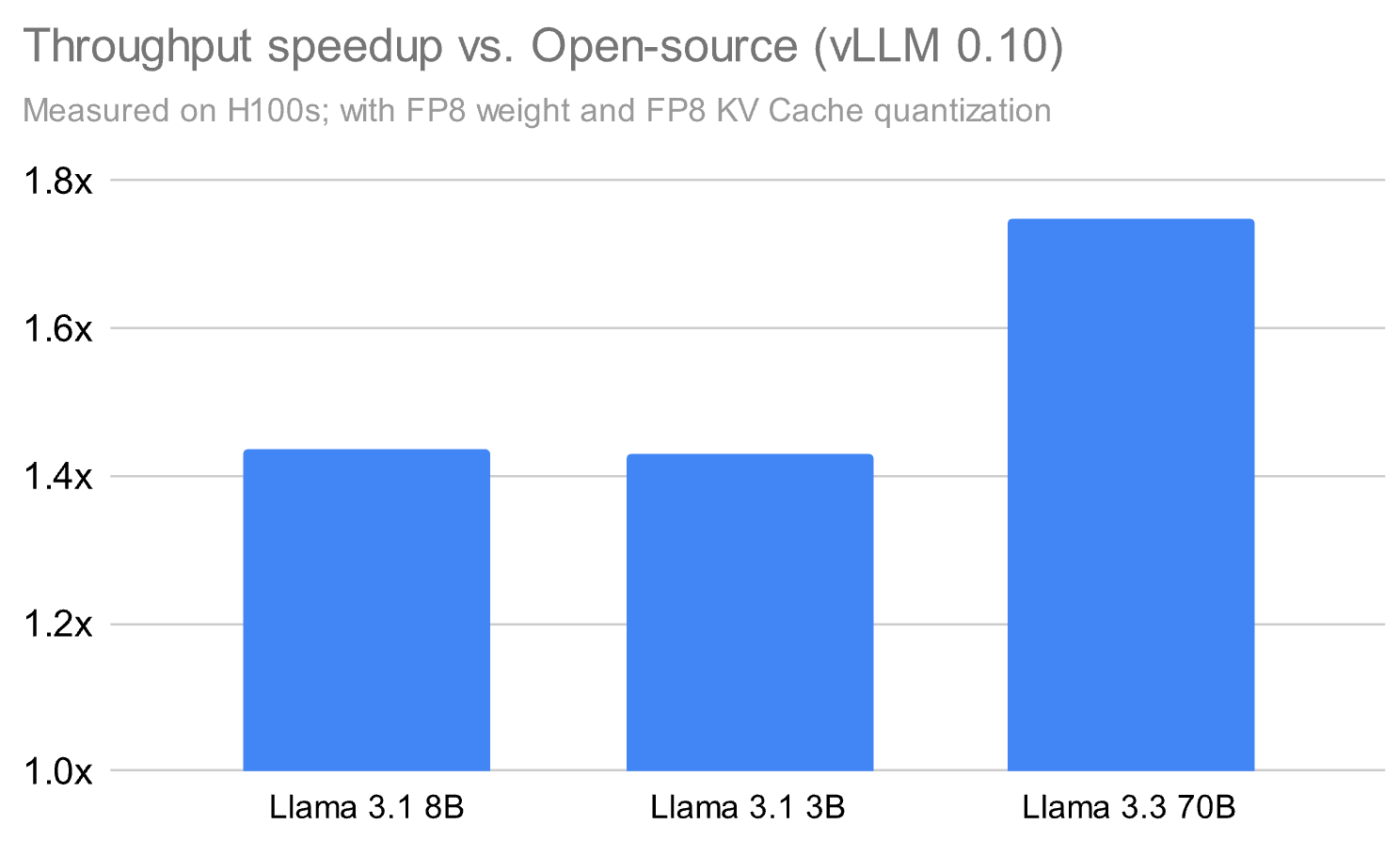
Beyond the inference runtime itself, we've built a comprehensive serving infrastructure that addresses the full production stack: scalability, reliability, and fault tolerance. This involved solving complex distributed systems challenges including auto-scaling and load balancing, multi-region deployment, health monitoring, intelligent request routing and queuing, distributed state management, and enterprise-grade security controls.

Through this, our customers achieve not just fast inference, but a production-ready system that handles real-world enterprise workloads with the reliability and scale they demand. While we’ve made many innovations to achieve this performance, from custom kernels to optimized runtimes, in this blog we will focus on just one of those directions: fast serving of fine-tuned models with LoRA.

Here are the key principles that guided our work:

• Think framework-first, not kernel-first: The most effective optimizations emerge when you zoom out—understanding how scheduling, memory, and quantization all interact across layers of the stack.
• Quantization must respect model quality: Leveraging FP8 can unlock massive speedups, but only if paired with hybrid formats and fused kernels that preserve accuracy.
• Overlap is a throughput multiplier: Whether it’s overlapping kernels across streams or within the same stream using SM throttling, maximizing GPU utilization is key to maximizing throughput.
• CPU overheads are often the silent bottleneck: Especially for smaller models, inference performance is increasingly gated by how fast the CPU can prepare and dispatch work to the GPU. It is also important to minimize the idle GPU time between two decode steps by overlapping CPU execution with GPU execution.

Diving Deeper Into Fast Serving of Fine-Tuned Models

Among many parameter-efficient finetuning (PEFT) techniques, LoRA has emerged as the most widely adopted PEFT method due to its balance of quality preservation and computational efficiency. Recent research, including the comprehensive "LoRA Without Regret" study by Schulman et al. and our own study “LoRA learns less, forgets less”, has validated key principles for effective LoRA usage: apply LoRA to all layers (especially MLP/MoE layers) and ensure sufficient adapter capacity relative to dataset size. However, achieving good compute efficiency at inference requires significantly more than just following these principles. The theoretical FLOP advantages of LoRA don't automatically translate to real-world performance gains due to numerous inference-time overheads.

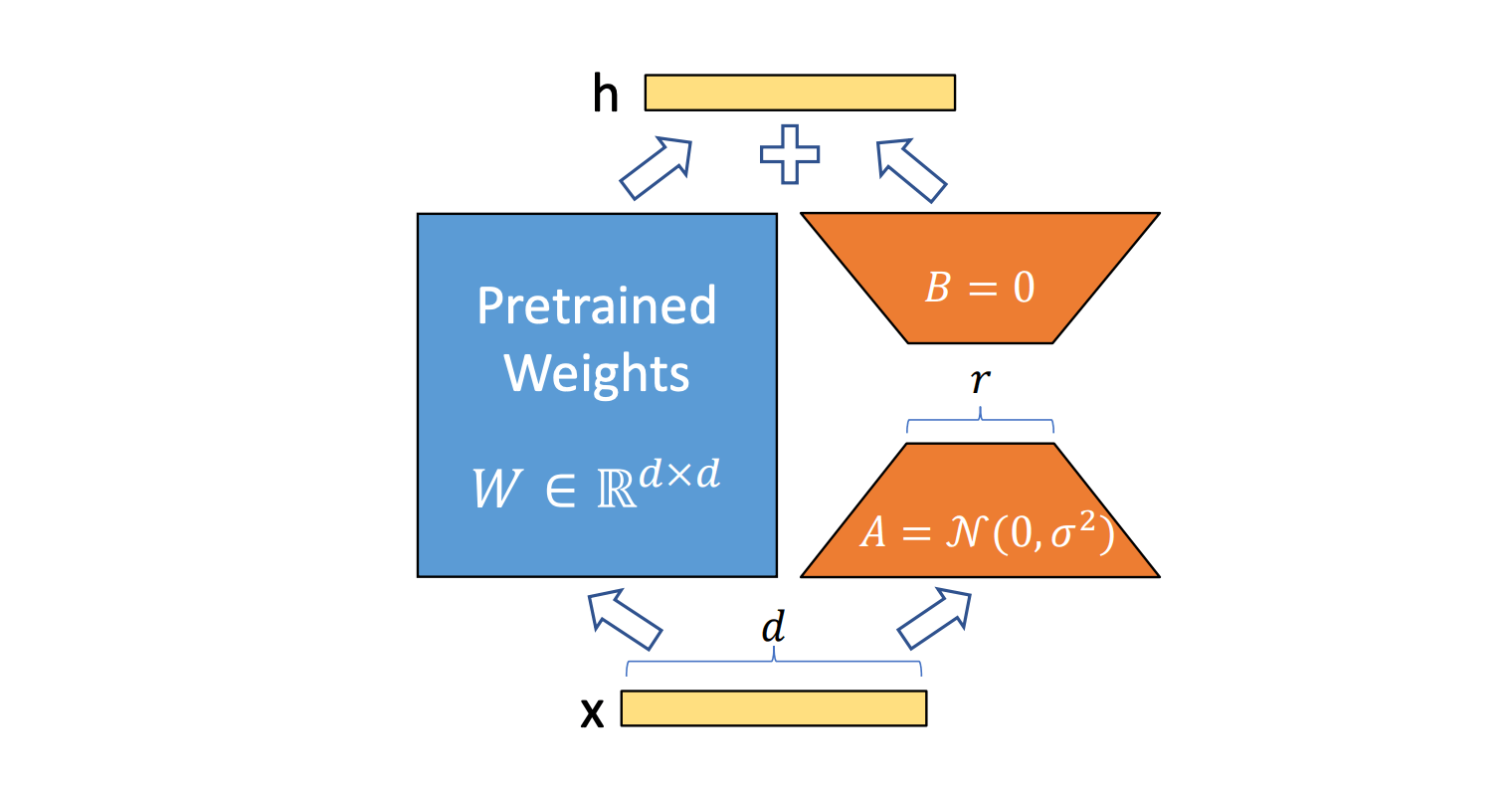
Moreover, there is a trade-off between the LoRA rank, which impacts the quality of the final model, and model inference performance. Based on our experiments, we found that for most customers, a higher rank of 32 was necessary to not degrade model quality during training. But this introduces pressure on the inference system to optimize.

In production systems, servers must handle a varying number of LoRA requests, which is a challenging problem to optimize for performance. Existing approaches have significant overheads when serving LoRA, sometimes slowing inference up to 60% in realistic scenarios.  

During inference, LoRA adapters are applied as low-rank matrix multiplications for each of the individual adapters and for each token in parallel with the base model’s linear layers. These matrix multiplications typically involve smaller inner and outer dimensions than the dimensions observed for models in the open source community. For instance, common hidden dimensions for open source models like the Llama 3.1 8B model are 8192 whereas the rank dimension can be as low as 8 for LoRA matrix multiplications. As such, the open source community has not invested significant efforts in optimizing their kernels for these setups and in techniques to maximize their hardware utilizations for these scenarios. 

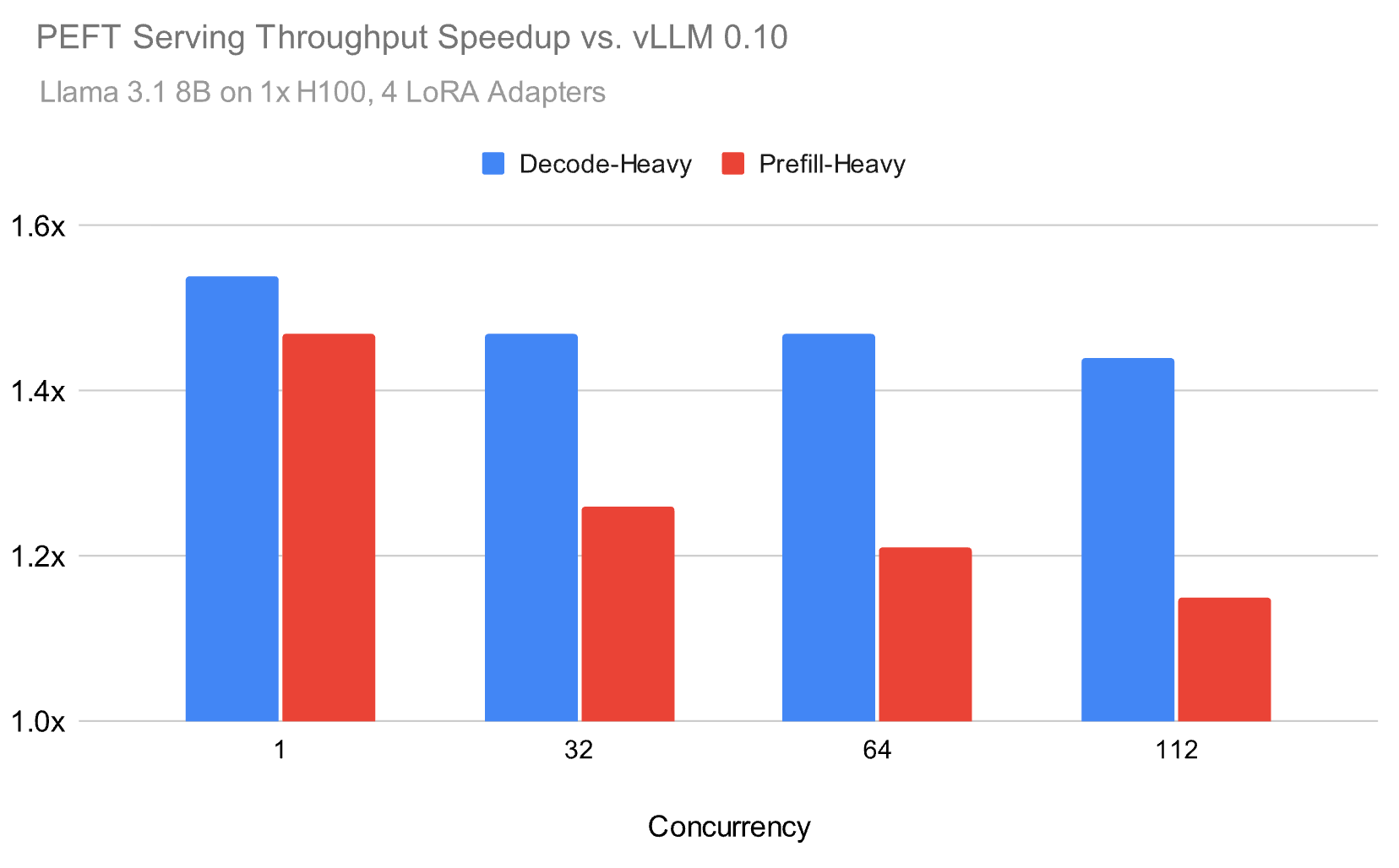
Over the past year, we developed our inference runtime to address these challenges, and as illustrated in Figure 1, we are able to achieve up to 1.5x speed-up on serving LoRA in realistic environments compared to the open source. For example, below we benchmark the Meta Llama 3.1 8B model using a Zipf distribution for the LoRA adapters with an average of 4 adapters.  

Our inference runtime achieves up to 1.5x higher throughput than popular open source alternatives for both prefill-heavy and decode-heavy workloads, with the performance gap narrowing but remaining substantial at higher loads. In order to achieve these speed-ups, we focused on a few components that we describe in this blog:

• Quality is just as important as performance optimizations. We were able to maximize performance with custom Attention and GEMM implementations, while preserving the model quality on key benchmarks.
• Partitioning GPU resources both across and within multi-processors to better handle the small matrix multiplications in GEMM.
• Optimizing overlap of kernel executions to minimize bottlenecks in the system.

Quantization that Preserves Base Model Quality

Quantization to take advantage of lower precision hardware units is key to performance, but can have an impact on quality. Model providers typically compress their models to fp8 during inference. Conversely, training is more quality sensitive so fine-tuning of LoRA adapters is typically performed on models in their native precision (bf16). This discrepancy leads to a challenge for serving PEFT models, where we must maximize the hardware resources while ensuring that the quality of the base model is preserved during inference to best mimic training settings.

In order to retain quality while optimizing performance, we developed some custom techniques into our custom runtime. As seen in the table below, our optimizations can retain the quality of the trained adapters compared to serving in full precision. This is one of the reasons our runtime is not only faster, but also has higher quality on benchmarks compared to open source runtimes.

Figure 4, With our custom changes, we are able to more closely retain the quality from a baseline where the base model is served in BF16. Note that all measurements with vLLM 0.10 are made with their FP8 tensorwise weight, dynamic activation, and KV cache quantization enabled. 

Rigorous Quality Validation

A key lesson from productionizing quantization is the need for rigorous quality validation. At Databricks, we don’t just benchmark models—we run detailed statistical comparisons between quantized and full-precision outputs to ensure that no perceptible degradation occurs. Every optimization we deploy must meet this bar, regardless of the performance gain it provides.

Quantization must also be treated as a framework-level concern, not a local optimization. By itself, quantization can introduce overheads or bottlenecks. But when coordinated with kernel fusion or in-kernel processing techniques like warp specialization, those overheads can be hidden entirely—yielding both quality and performance. In the section below, we dive into specific quantization strategies that made this possible.

FP8 Weight Quantization

There are numerous approaches to be able to quantize the weights of a model, each with their own set of tradeoffs. Some quantization techniques are more granular in the placement of their scale factors whereas others are coarse-grained. These coarse-grained approaches result in higher error but less overhead during the quantization of the activation tensors.

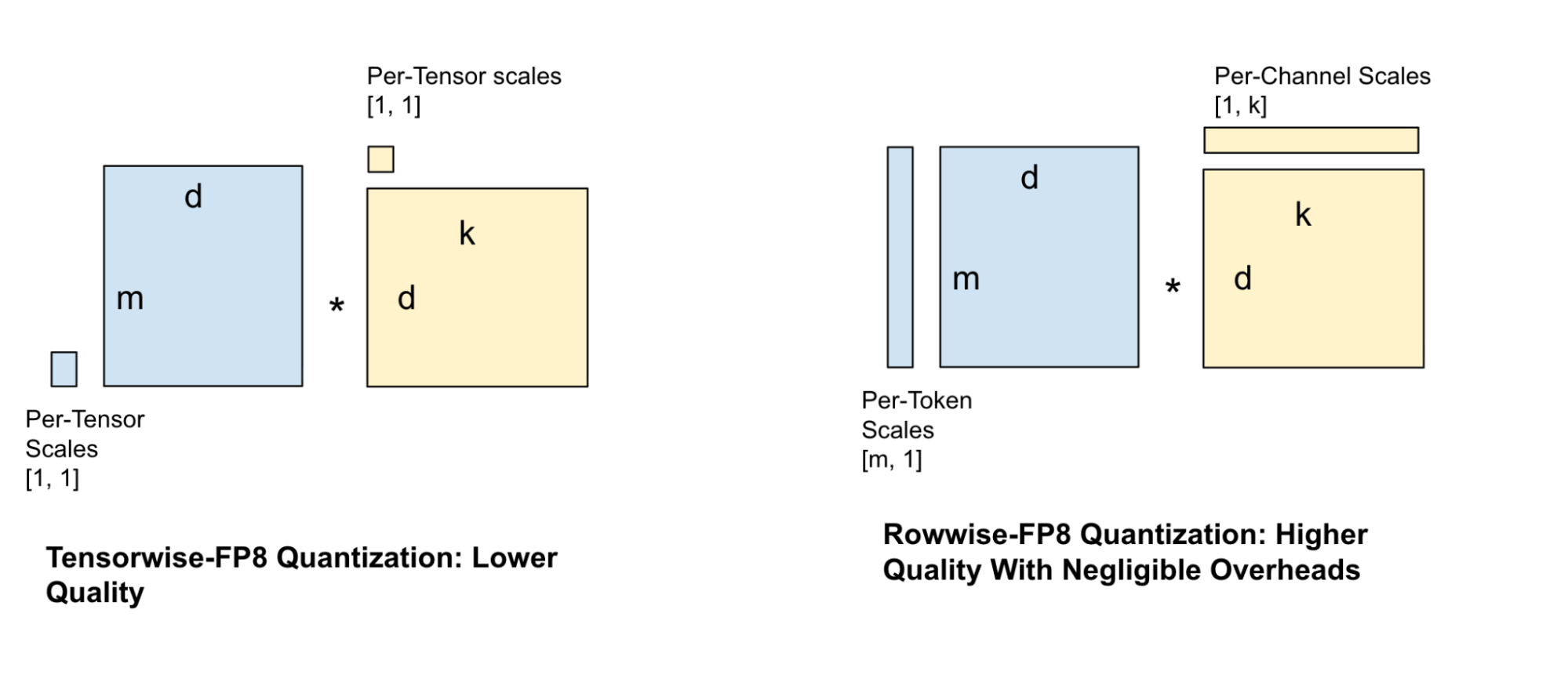
A popular quantization technique for serving models is tensor-wise FP8 quantization, where one scale factor is assigned to the entire tensor. However, this technique is quite lossy and results in significant quality reduction, especially for smaller models. This necessitates more granular scale factors, which led us to try various scale factor configurations for the weights and activations such as per-channel and per-block scales. Balancing GEMM speed against quality loss, we chose the rowwise scale factor configuration as shown in Figure 4.

To overcome the performance overhead of calculating more granular scale factors for the activations, we perform some critical kernel fusions with preceding bandwidth-bound operations to hide the overhead of the additional compute.

Hybrid Attention

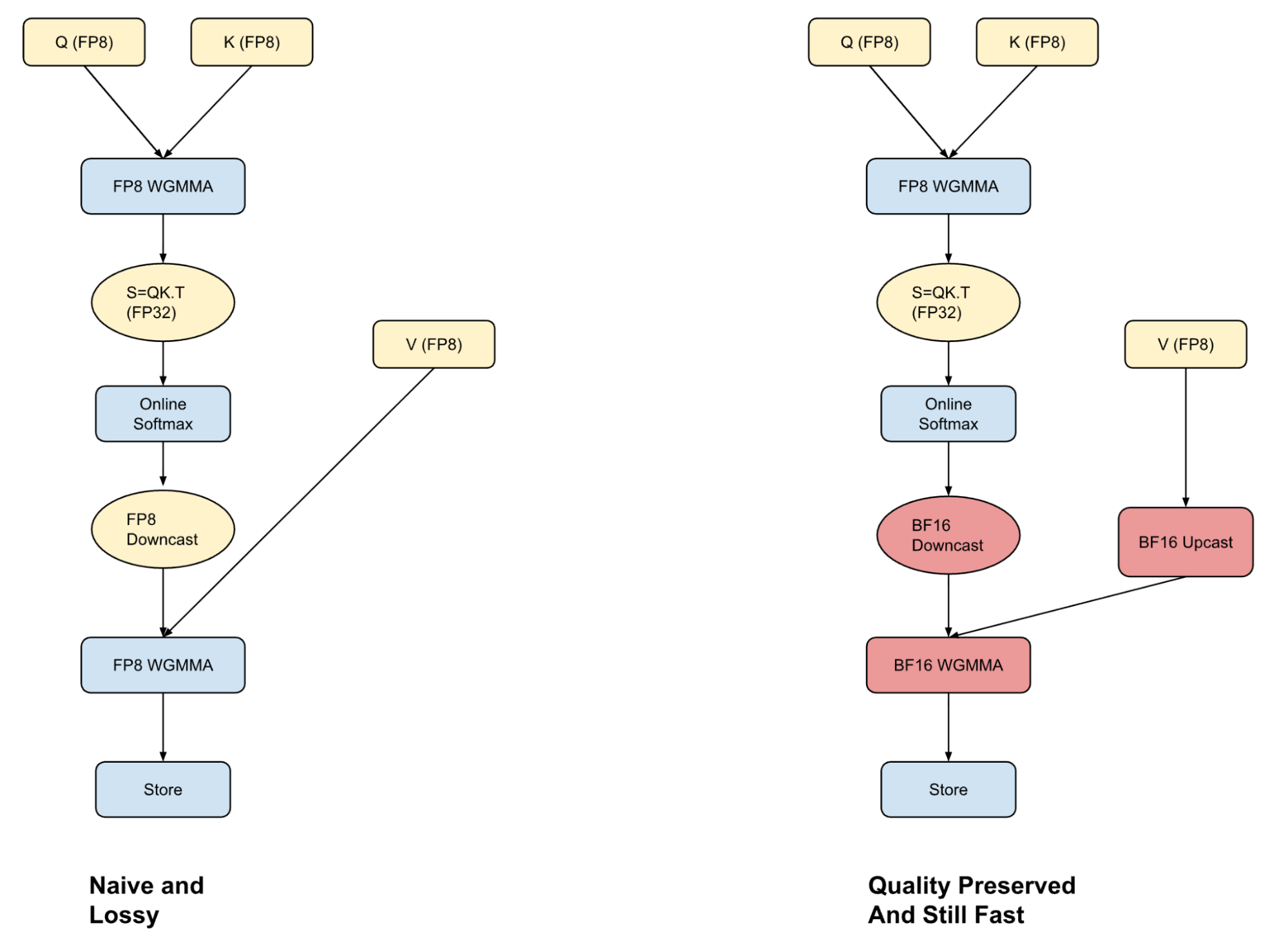
A core part of Transformer-based inference is the Attention operation, which can take up to 50% of the total computation time for smaller models at long context lengths. One common approach to speed decodes during inference is to cache the Key value outputs from the prefill. 

Storing KV caches in FP8 format can improve throughput, but unlocking the full benefit requires an attention kernel that can handle FP8 inputs accurately and fast. Most frameworks either perform attention entirely in FP8 (fast but lossy) or use BF16 (more accurate but slower due to upcasting). We’ve taken a middle path with hybrid attention—we blend the strengths of both formats to achieve a better trade-off between performance and quality. 

We converged to this format after finding that the quantization error in the FP8 attention computation comes from downcasting the softmax computation to a lower bit representation. By performing the first part of the computation in FP8 and by exploiting warp specialization strategies on Hopper GPUs, we can overlap the upcast of the V-vector with the Q-K computation. This then allows us to run the P-V computation in BF16 without any performance penalty. While this is still slower than doing all computation in FP8, more importantly the hybrid approach does not degrade the model quality. 

Our work builds on similar approaches suggested in Academia, SageAttention and SageAttention2 by Zhang et al., as well as in a blog from CharacterAI.

Post-RoPE Fused Fast Hadamard Transforms

Recall that the query and key for a given token are computed from its embedding x at the start of the attention module as:

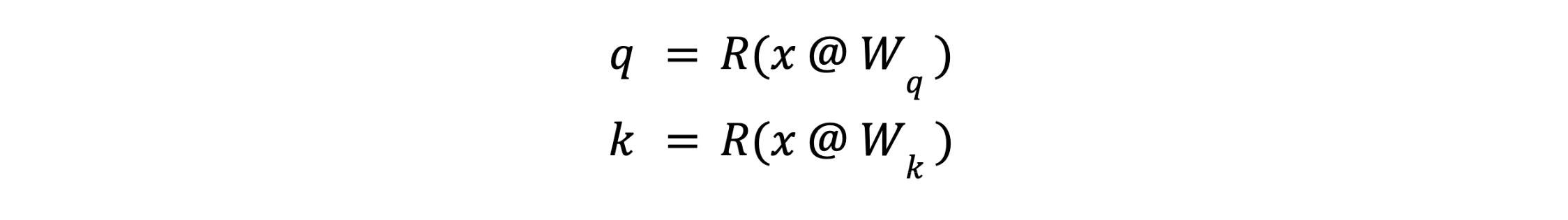
Where R() is the RoPE embedding operator. After RoPE, it is not necessary to preserve the exact values of q or k–it is only necessary to preserve the inner products q.T @ k for all queries q and keys k. This lets us apply a linear transform U to q and k:

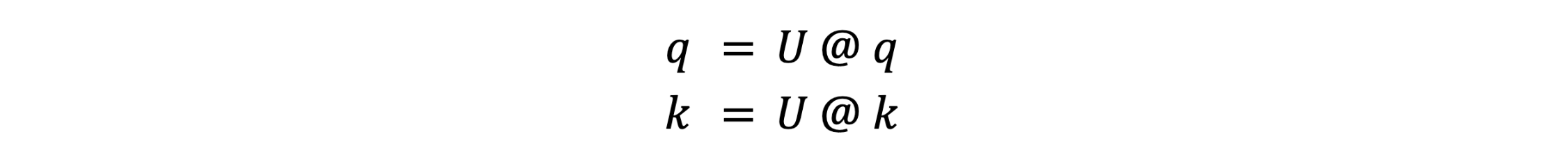
such that U.T @ U = I, the identity matrix. This makes U cancel out during the attention computation:

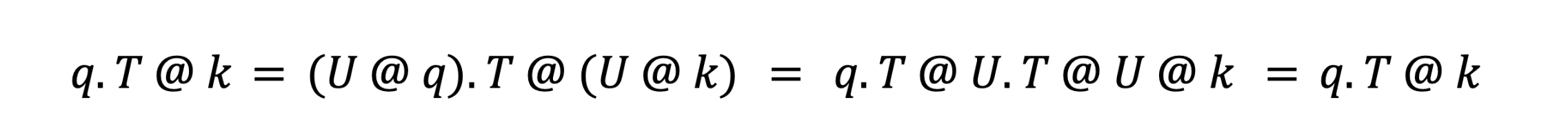
This lets us optimize the q and k vectors for quantizability without (mathematically) changing the attention computation. The specific transform we use is the Fast Hadamard Transform (FHT), which lets us spread variance across D channels in O(log2(D)) operations. This spreading of variance eliminates outliers and enables smaller FP8 scales–you can think of this being able to “zoom in” for better resolution. This work builds on similar approaches suggested in Academia, FlashAttention3 by Dao et al,, and QuaRot by Ashkboos et al. 

To avoid overhead, we wrote a kernel that fuses RoPE, the FHT, quantization, and appending to the KV cache.

Overlapping Kernels To Minimize PEFT Overheads

During inference with LoRA, the adapter rank represents one of the dimensions of the matrix multiplication. Since the rank typically can be small (e.g. 8 or 32), this leads to matrix-multiplications with skewed dimensions, resulting in additional overhead during inference (Figure 1). 

As such, inspired from the Nanoflow work by Zhu et al., we have been exploring various strategies to hide this overhead by overlapping LoRA kernels with the base model and between themselves. 

As described in Figure 1, LoRA inferencing consists of two main kernels, a down-projection kernel (defined as the “Shrink” kernel) and an up-projection kernel (defined as the “Expand” kernel). These are primarily Grouped GEMMs (where each GEMM operates on a different adapter) since we typically serve multiple LoRA adapters simultaneously. This allows us to overlap these Grouped GEMMs with the base model’s computations and the Shrink, Expand kernels between each other as described below in Figure 6.

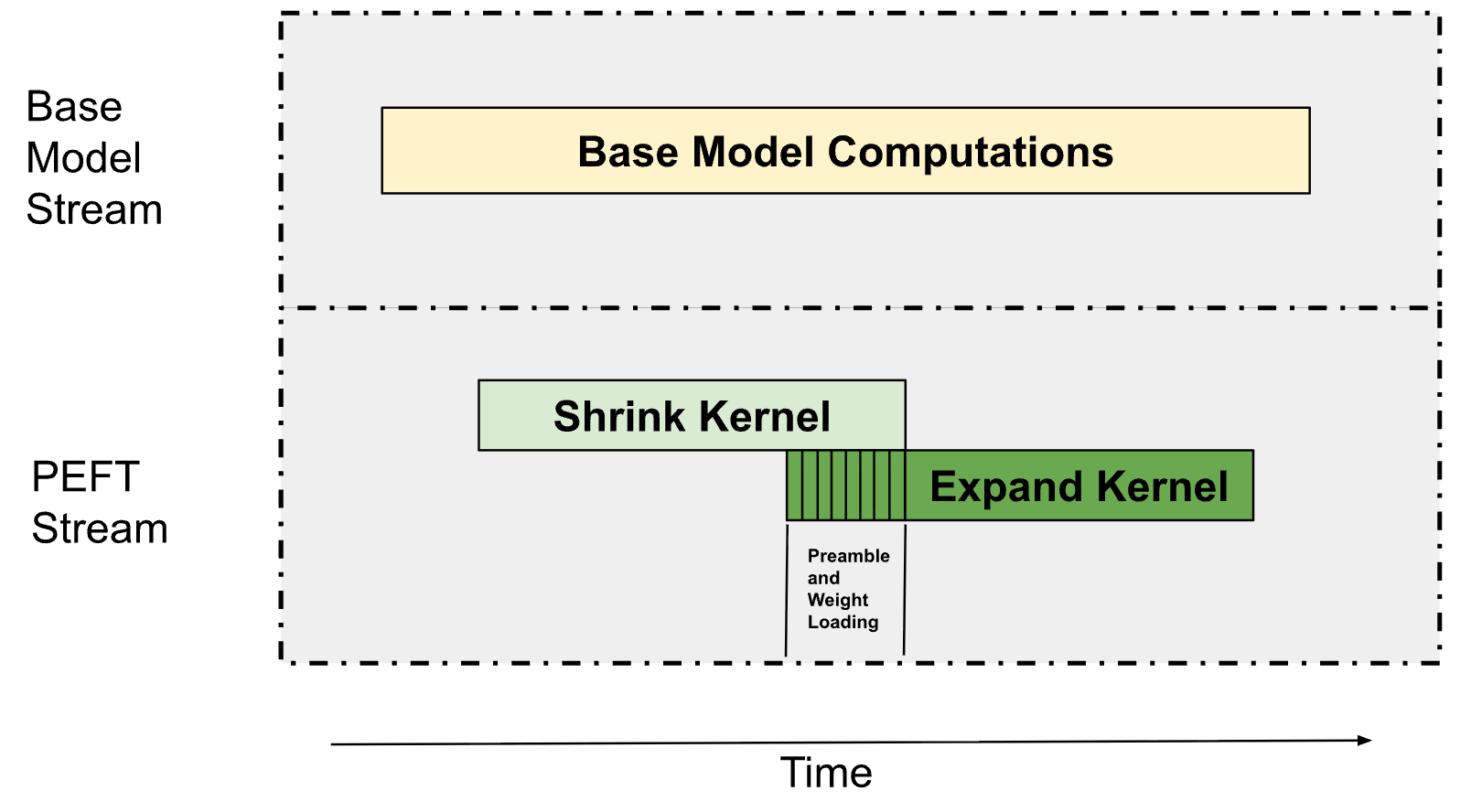
Parallel Streams with Multiprocessor Partitioning

At a surface level, it is trivially possible to overlap kernel executions that depend on different data by launching them in separate streams. This approach inherently relies on the compute work distributor to schedule the blocks of the different kernel executions. However, this only works when there's sufficient unused compute capacity. For larger workloads that would normally saturate the GPU, we need a more sophisticated approach.

Going beyond this, we realized that we can partition the number of Streaming Multiprocessors (SMs) required by bandwidth bound kernels without significantly affecting their performance. In most scenarios, we have found that bandwidth-bound kernels do not need all the possible SMs in order to be able to access the full memory bandwidth on the GPU. As such, this allows us to restrict the number of SMs used by these kernels and then use the remaining multi-processors to perform other computations.

For PEFT, we run two streams, one for the base model and one for the PEFT path. The base model receives as high as 75% of the SMs on the GPU and the remaining go to the PEFT path, With this partitioning, we have found that the base model path does not slow down significantly whereas the PEFT path is able to run in the background allowing us to hide the overhead from PEFT in most cases.

Same Stream with Dependent Launches

While kernel executions that depend on different data can be easily overlapped across different streams, dependent kernel executions in the same stream are harder to overlap since each kernel must wait for the previous one to complete. To address this, we use Programmatic Dependent Launch (PDL), which allows us to pre-fetch the weights for the next kernel while the current one is still executing.

PDL is an advanced CUDA runtime feature that enables launching a dependent kernel before the primary kernel in the same stream has finished executing. This is illustrated in Figure 8 below.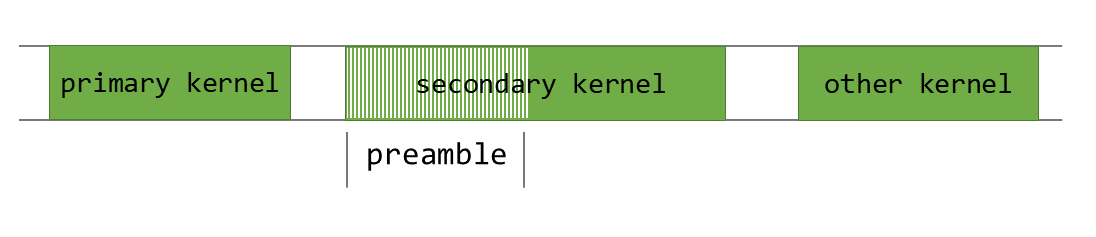

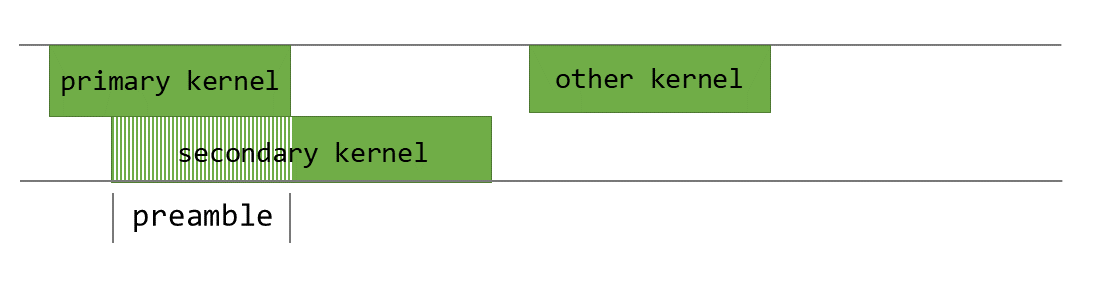
For our PEFT kernels, we use PDL to overlap the shrink and expand operations. While the shrink kernel executes, we pre-fetch the weights needed for the Expand kernel into shared memory and the L2 cache. We throttle the shared memory and the register resources of the Shrink kernel to ensure that there are enough resources for the Expand kernel to run. This allows the Expand kernel to begin weight processing while the Shrink kernel is still completing its computation. Once the Shrink kernel is complete, the Expand kernel loads the activations and starts performing the matrix multiplication computations. 

Conclusion

Allowing our customers to leverage their data to drive unique insights is a core part of our strategy here at Databricks. A key part of this is being able to successfully serve LoRA requests in the inference runtime. The techniques we’ve shared —from quantization formats to kernel fusion, from SM-level scheduling to CPU-GPU overlap, all stem from this framework-first philosophy. Each optimization was validated against rigorous quality benchmarks to ensure we never traded accuracy for speed.

As we look ahead, we’re excited to push further with more megakernel strategies and smarter scheduling mechanisms.

To get started with LLM inference, try out Databricks Model Serving on our platform.

Authors: Nihal Potdar, Megha Agarwal, Hanlin Tang, Asfandyar Qureshi, Qi Zheng, Daya Khudia